Thermal-Hydraulic-Mechanical-Chemical (THMC) coupling
& Hydraulic-mechanical-damage (HMD) coupling
TDBORE solver 3D v1.1 for damage evolution, multi-fields coupling and wellbore stability
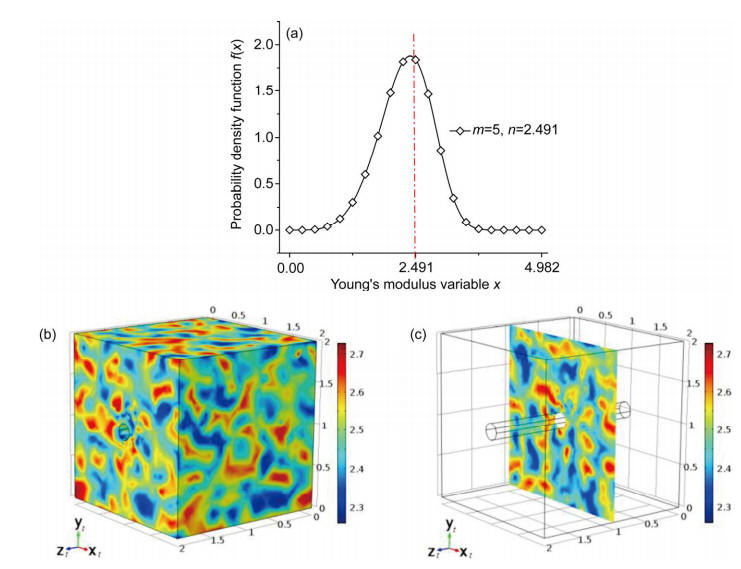
The finite element analysis (FEA) technology by hydraulic-mechanical-chemical-damage (HMCD) coupling is proposed in this paper for inclined wellbore stability analysis of water-sensitive and laminated rock, developed basing on the recently established FEA technology for transversely isotropic rock with hydraulic-mechanical-damage (HMD) coupling. The chemical activity of the drilling fluid is considered as phenomenological hydration behavior, the moisture content and parameters of rock considering hydration could be determined with time. The finite element (FE) solutions of numerical wellbore model considering the chemical activity of drilling fluid, damage tensor calculation and weak plane strength criterion for transversely isotropic rock are developed for researching the wellbore failure characteristics and computing the time-dependent collapse and fracture pressure of laminated rock as shale reservoirs. A three-dimensional FE model and elastic solid deformation and seepage flow coupled equations are developed, and the damage tensor calculation technology for transversely isotropic rock are realized by introducing effect of the hydration and the stress state under the current load. The proposed method utilizing weak plane strength criterion fully reflects the strength parameters in rock matrix and weak plane. To the end, an effective and reliable numerically three-step FEA strategy is well established for wellbore stability analysis. Numerical examples are given to show that the proposed method can establish efficient and applicable FE model and be suitable for analyzing the timedependent solutions of pore pressure and stresses, and the evolution region considering the hydration surrounding wellbore, furthermore to compute the collapse cycling time and the safe mud weight for collapse and fracture pressure of transversely isotropic rock.

& Hydraulic-mechanical (HM) coupling
Adaptive FE-DE-FV solver 3D to be released...
& IRAZU GEOMECHANICA simulation software
Link to IRAZU GEOMECHANICA simulation software at University of Toronto
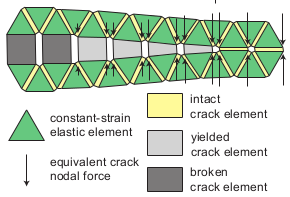
Geomechanica¨s Irazu simulation software is a state-of-the-art simulation tool based on the hybrid finite-discrete element method (FEMDEM or FDEM), a numerical method which combines continuum mechanics principles with discrete element method (DEM) algorithms to simulate multiple interacting deformable bodies. In Irazu, each solid is discretized as a mesh consisting of nodes and triangular elements. An explicit time integration scheme is applied to solve the equations of motion for the discretized system and to update the nodal coordinates at each simulation time step.
MATERIAL DEFORMATION AND
FRACTURING
The progressive
failure of intact rock material is modelled using a cohesive-zone approach,
which aims at capturing the non-linear interdependence between stresses and
strain that characterizes the zone ahead of a macro-crack tip known as the
Fracture Process Zone (FPZ). When using cohesive-zone models, the failure of the
material progresses based solely on the strength degradation of dedicated
interface elements (known as crack elements) and therefore emerges as a natural
outcome of the deformation process without employing any additional macroscopic
failure criterion. Since the material strain is expected to be localized in the
cohesive zone, the bulk material (i.e., the continuum, or unfractured, portion
of the model) is treated as linear-elastic using constant-strain triangular
elements. The bonding stresses transferred by the material are decreasing
functions of the displacement discontinuity across the crack elements. Both Mode
I and Mode II failure can be reproduced. In Irazu, the crack elements are
interspersed throughout the material (i.e, across the edges of all triangular
element pairs) from the very beginning of the simulation. Thus, cracks are
allowed to nucleate and grow without any additional assumption or criterion
other than the crack element constitutive response. Upon breakage of the
cohesive surface, the crack element is removed from the simulation and therefore
the model locally transitions from a continuous to a discontinuous statew. As
the simulation progresses, finite displacements and rotations of discrete bodies
are allowed and new contacts are automatically recognized.
CONTACT DETECTION AND INTERACTION
An Irazu simulation
can comprise a very large number of potentially interacting distinct elements.
To correctly capture this behaviour, contacting couples (i.e., pairs of
contacting discrete elements) must first be detected. Subsequently, the
interaction forces resulting from such contacts can be defined. Contact
interaction forces are calculated between all pairs of elements that overlap in
space. Two types of forces are applied to the elements of each contacting pair:
repulsive forces and frictional forces. The repulsive forces between the
elements of each contacting pair (i.e., couples) are calculated using a penalty
function method. The frictional forces between contacting couples are calculated
using a Coulomb-type friction law. These frictional forces are used to simulate
the shear strength of intact material and of pre-existing and newly-created
fractures.
& THERMAID simulation software
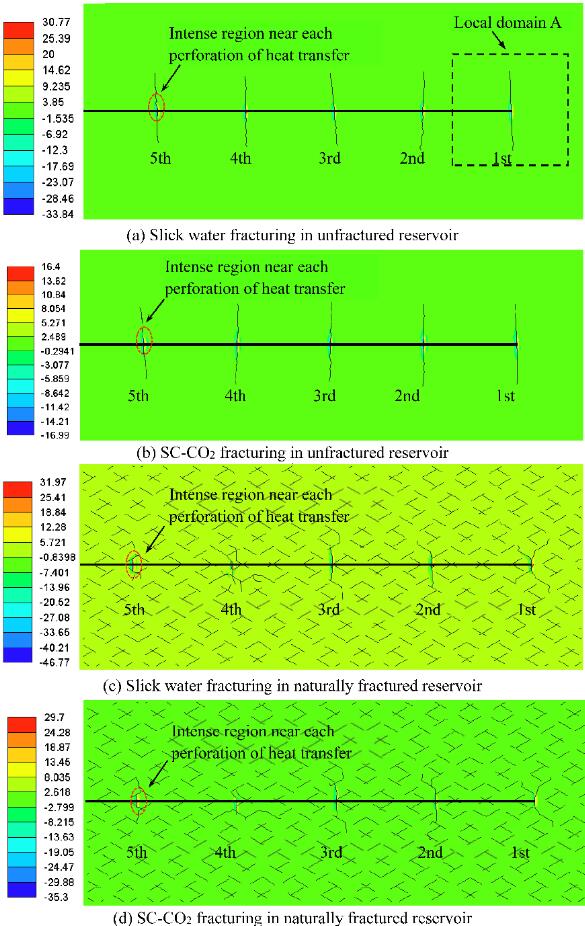
& Thermal effects in SC-CO2 fracturing
References of numerical and experimental analysis

& SC-CO2 fracturing considering thermal-hydro-mechanical coupling
References of numerical and experimental analysis